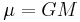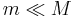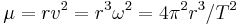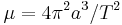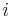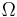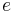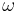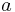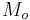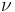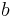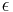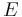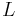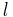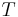Standard gravitational parameter
| Body | μ (km3s−2) |
|---|---|
| Sun | 132,712,440,018(8)[1] |
| Mercury | 22,032 |
| Venus | 324,859 |
| Earth | 398,600.4418(9) |
| Moon | 4,902.7779 |
| Mars | 42,828 |
| Ceres | 63.1(3)[2][3] |
| Jupiter | 126,686,534 |
| Saturn | 37,931,187 |
| Uranus | 5,793,939(13)[4] |
| Neptune | 6,836,529 |
| Pluto | 871(5)[5] |
| Eris | 1,108(13)[6] |
In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.
The SI units of the standard gravitational parameter are m3s−2.
Contents |
Small body orbiting a central body
Under standard assumptions in astrodynamics we have:
where m is the mass of the orbiting body, M is the mass of the central body, and G is the standard gravitational parameter of the larger body.
For all circular orbits around a given central body:
where r is the orbit radius, v is the orbital speed, ω is the angular speed, and T is the orbital period.
The last equality has a very simple generalization to elliptic orbits:
where a is the semi-major axis. See Kepler's third law.
For all parabolic trajectories rv2 is constant and equal to 2μ. For elliptic and hyperbolic orbits μ = 2a|ε|, where ε is the specific orbital energy.
Two bodies orbiting each other
In the more general case where the bodies need not be a large one and a small one (the two-body problem), we define:
- the vector r is the position of one body relative to the other
- r, v, and in the case of an elliptic orbit, the semi-major axis a, are defined accordingly (hence r is the distance)
- μ = Gm1 + Gm2 = μ1 + μ2, where m1 and m2 are the masses of the two bodies.
Then:
- for circular orbits, rv2 = r3ω2 = 4π2r3/T2 = μ
- for elliptic orbits, 4π2a3/T2 = μ (with a expressed in AU and T in years, and with M the total mass relative to that of the Sun, we get a3/T2 = M)
- for parabolic trajectories, rv2 is constant and equal to 2μ
- for elliptic and hyperbolic orbits, μ is twice the semi-major axis times the absolute value of the specific orbital energy, where the latter is defined as the total energy of the system divided by the reduced mass.
Terminology and accuracy
Note that the reduced mass is also denoted by 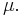 .
.
The value for the Earth is called the geocentric gravitational constant and equals 398,600.4418±0.0008 km3s−2. Thus the uncertainty is 1 to 500,000,000, much smaller than the uncertainties in G and M separately (1 to 7,000 each).
The value for the Sun is called the heliocentric gravitational constant and equals 1.32712440018×1020 m3s−2.
References
- ^ "Astrodynamic Constants". NASA/JPL. 27 February 2009. http://ssd.jpl.nasa.gov/?constants. Retrieved 27 July 2009.
- ^ E.V. Pitjeva (2005). "High-Precision Ephemerides of Planets — EPM and Determination of Some Astronomical Constants". Solar System Research 39 (3): 176. Bibcode 2005SoSyR..39..176P. doi:10.1007/s11208-005-0033-2. http://iau-comm4.jpl.nasa.gov/EPM2004.pdf.
- ^ D. T. Britt, D. Yeomans, K. Housen, G. Consolmagno (2002). "Asteroid density, porosity, and structure". In W. Bottke, A. Cellino, P. Paolicchi, R.P. Binzel. Asteroids III. University of Arizona Press. p. 488. http://www.lpi.usra.edu/books/AsteroidsIII/pdf/3022.pdf.
- ^ R.A. Jacobson, J.K. Campbell, A.H. Taylor, S.P. Synnott (1992). "The masses of Uranus and its major satellites from Voyager tracking data and Earth-based Uranian satellite data". Astronomical Journal 103 (6): 2068–2078. Bibcode 1992AJ....103.2068J. doi:10.1086/116211.
- ^ M.W. Buie, W.M. Grundy, E.F. Young, L.A. Young, S.A. Stern (2006). "Orbits and photometry of Pluto's satellites: Charon, S/2005 P1, and S/2005 P2". Astronomical Journal 132: 290. arXiv:astro-ph/0512491. Bibcode 2006AJ....132..290B. doi:10.1086/504422.
- ^ M.E. Brown, E.L. Schaller (2007). "The Mass of Dwarf Planet Eris". Science 316 (5831): 1585. Bibcode 2007Sci...316.1585B. doi:10.1126/science.1139415. PMID 17569855. http://www.sciencemag.org/cgi/content/full/316/5831/1585.